Kartezyen koordinatlarda vektör alanının diverjans aşağıdaki gibi tanımlanıyor. $$\mathbf F = (F_x, F_y, F_z)$$
$$\nabla\cdot \mathbf F = \left(\frac {\partial} {\partial x},\frac {\partial} {\partial y},\frac {\partial} {\partial z}\right)\cdot\left(F_x, F_y, F_z\right) = \frac {\partial F_x} {\partial x}+\frac {\partial F_y}{\partial y}+\frac {\partial F_z} {\partial z}$$
Kartezyen koordinatlar cinsinden silindirik koordinat birim vektörleri tanımlanabilir.
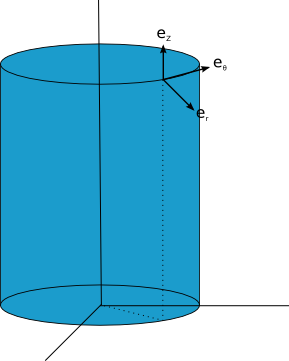
Silindirik koordinatlar $r$, $\theta$,$z$ cinsinden tanımları:
$$x = r.cos(\theta)$$ $$y = r.sin(\theta)$$ $$z = z$$
$\mathbf{e_z}$, $\mathbf k$ ile aynı: $ \mathbf{e_z} = (0, 0, 1)$
$$ \mathbf{e_r} = \frac {\left(x, y, 0\right)} {\sqrt{x^2+y^2}} = \frac {\left(r.cos\left(\theta\right), r.cos\left(\theta\right), 0\right)} {r} = (cos(\theta), sin(\theta), 0)$$
$\mathbf{e_\theta}$ ise bu iki vektörün vektörel çarpımına eşittir.
$$ \mathbf{e_\theta} = e_z \times e_r = \frac {(-y, x, 0)} {\sqrt{x^2+y^2}} =(-sin(\theta), cos(\theta), 0)$$
Şimdi vektör alanını x, y ve z yerine $r$, $\theta$,$z$ şeklinde yazabiliriz.
$$ \mathbf F = (F_r, F_\theta, F_z) = F_re_r + F_\theta e_\theta + F_ze_z$$ $$\mathbf F = F_r(cos\theta, sin\theta, 0) + F_\theta(-sin\theta, cos\theta, 0) + F_z(0, 0, 1)$$ $$\mathbf F = (F_rcos\theta - F_\theta sin \theta, F_rsin\theta + F_\theta cos \theta, F_z)$$
Şimdi del operatörünü $r$, $\theta$,$z$ cinsinden yazmak için zincir kuralını kullanacağız.
$$ \frac {\partial} {\partial r} = \frac {\partial} {\partial x} \frac {\partial x} {\partial r} + \frac {\partial} {\partial y} \frac {\partial y} {\partial r} $$ $$ \frac {\partial} {\partial \theta} = \frac {\partial} {\partial x} \frac {\partial x} {\partial \theta} + \frac {\partial} {\partial y} \frac {\partial y} {\partial \theta} $$
Aşağıdaki türevleri biliyoruz.
$$ \frac {\partial x} {\partial r} = cos\theta\\ \frac {\partial y} {\partial r} = sin\theta\\ \frac {\partial x} {\partial \theta} = -r.sin\theta\\ \frac {\partial y} {\partial \theta} = r.cos\theta $$ Bunları yerlerine koyup gerekli düzenlemeleri yaparsak del operatörü aşağıdaki gibi olur.
$$ \nabla = \left( \frac 1 r \left( r.cos\theta\frac {\partial} {\partial r} -sin\theta\frac {\partial x} {\partial \theta}\right), \frac 1 r \left( r.sin\theta\frac {\partial} {\partial r} +cos\theta\frac {\partial x} {\partial \theta}\right), \frac {\partial} {\partial z}\right) $$
O zaman diverjans formülü şu şekilde yazılabilir.
$$ \nabla\cdot F = \left( \frac 1 r \left( r.cos\theta\frac {\partial} {\partial r} -sin\theta\frac {\partial x} {\partial \theta}\right), \frac 1 r \left( r.sin\theta\frac {\partial} {\partial r} +cos\theta\frac {\partial x} {\partial \theta}\right), \frac {\partial} {\partial z}\right)\cdot (F_rcos\theta - F_\theta sin \theta, F_rsin\theta + F_\theta cos \theta, 0) $$
Açılınca ise
$$ \nabla\cdot F = \frac 1 r \frac {\partial} {\partial r} F_r r.cos^2\theta\\ - \frac 1 r \frac {\partial} {\partial r}F_\theta cos\theta sin\theta\\ - \frac 1 r \frac {\partial} {\partial \theta} F_r cos\theta sin\theta\\ + \frac 1 r \frac {\partial} {\partial \theta}F_\theta sin^2\theta\\ + \frac 1 r \frac {\partial} {\partial r} F_r r.sin^2\theta\\ + \frac 1 r \frac {\partial} {\partial \theta}F_\theta cos\theta sin \theta\\ + \frac 1 r \frac {\partial} {\partial \theta}F_r cos\theta sin\theta\\ + \frac 1 r \frac {\partial} {\partial \theta}F_\theta cos^2\theta\\ + \frac {\partial} {\partial z} F_z $$
Böylece sonuç aşağıdaki gibi çıkıyor:
$$ \nabla\cdot F = \frac 1 r \frac {\partial (r.F_r)} {\partial r} + \frac 1 r \frac {\partial F_\theta} {\partial \theta} + \frac {\partial F_z} {\partial z} $$