Rıdvan Örsvuran

Küresel kosinüs kanunu ile dünya üzerindeki iki noktanın arasındaki uzaklığı hesaplayalım.

Bu iki noktanın birinin konumu (enlem1, boylam1) diğerinin konumu ise (enlem2, boylam2) olsun. Bir üçgen oluşturmak için bir noktaya daha ihtiyacımız var. Hesaplarda kolaylık sağlaması için coğrafik kuzey kutbunu alalım. Böylece küre yüzeyinde bir üçgen oluşturmuş olduk.

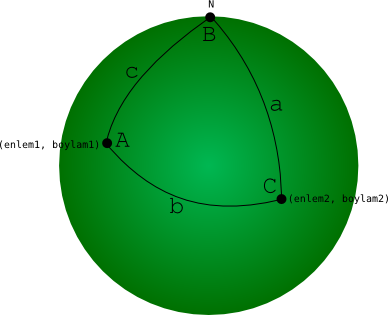
İki nokta arası uzaklık

Bu üçgenin iç açıları ve kenarları üstteki şekildeki gibi isimlendirilmiş olsun.

Küresel kosinüs kanunu bize aşağıdaki eşitliği veriyor. \begin{equation} cos(b) = cos(a)cos(c) + sin(a)sin(c)cos(B) \end{equation} Burada

• $B = \text{boylam2}-\text{boylam1}$
• $c = 90 - \text{enlem1}$
• $a = 90 - \text{enlem2}$

Bu eşitlikleri formül (1)'de yerine koyarsak iki nokta arasındaki uzaklık aşağıdaki gibi olur.

\begin{aligned} b &= cos^{-1}(cos(90 - \text{enlem2})cos(90 - \text{enlem1}) \\ &~~~~~~~~~~~~+ sin(90 - \text{enlem2})sin(90 -\text{enlem1}) cos(\text{boylam2}-\text{boylam1})) \end{aligned}

Bu formülü kısaltabiliriz.

• $cos(90 - x) = sin(x)$
• $sin(90 - x) = cos(x)$

olduğundan

\begin{aligned} b &= cos^{-1}(sin(\text{enlem2})sin(\text{enlem1}) \\ &~~~~~~~~~~~~+ cos(\text{enlem2})cos(\text{enlem1}) cos(\text{boylam2}-\text{boylam1})) \tag{2} \end{aligned}

Bu yazdığımız $b$ iki nokta arasındaki yayın açısını veriyor bize. Bu değeri yarıçap ile çarparsak uzunluğu buluyoruz.

\begin{aligned} \text{uzaklık} = R*cos^{-1}&(sin(\text{enlem1})sin(\text{enlem2}) \\ &+ cos(\text{enlem1})cos(\text{enlem2}) cos(\text{boylam2}-\text{boylam1}))\tag{3} \end{aligned}

İstanbul (41.004582, 28.977692) ile Ankara (39.920680, 32.854186) arasındaki uzaklığı bu formülle hesapladığımızda 349.36 km çıkıyor. ¹ (Çıkan sonucun kuş uçuşu mesafe olduğunu hatırlamak gerek.)

Azimut

Bir noktadan diğerine giderken kuzeyle yaptığımız açıya azimut diyoruz.

Sinüs kanunu yazalım. \begin{equation} \frac{sin(A)}{sin(a)} = \frac{sin(B)}{sin(b)} = \frac{sin(C)}{sin(c)} \tag{4} \end{equation} A'yı aşağıdaki gibi çekebiliriz. \begin{equation} A = sin^{-1}\left( \frac{sin(B)sin(a)}{sin(b)} \right) \tag{5} \end{equation}

Bildiğimiz değerler:

• $B = \text{boylam2}-\text{boylam1}$
• $a = 90 - \text{enlem2}$
• $sin(a) = sin(90 - \text{enlem2}) = cos(\text{enlem2})$
• $b$ yi ise (2) formülünden bulmuştuk.

Bunları yerine koyarsak

\begin{equation} A = sin^{-1}\left( \frac{sin(\text{boylam2}-\text{boylam1})cos(\text{enlem2})} {sin(b)} \right) \tag{6} \end{equation}

Yalnız bu açının değeri noktaların konumuna göre değişecek. Biz azimutu yani kuzeyle yapılan açıyı bulmak istiyoruz.

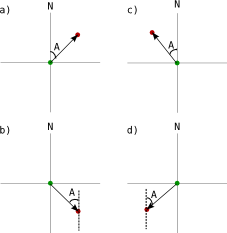
Resimde de görüldüğü gibi azimut (kuzeyle yapılan pozitif açı) \begin{equation} \text{azimuth} = \begin{cases} A & \text{enlem1} < \text{enlem2}, \text{boylam1} < \text{boylam2} \\ 180 - A & \text{enlem1} > \text{enlem2}, \text{boylam1} < \text{boylam2} \\ 360 + A & \text{enlem1} < \text{enlem2}, \text{boylam1} > \text{boylam2} \\ 180 + A & \text{enlem1} > \text{enlem2}, \text{boylam1} > \text{boylam2} \end{cases} \tag{7} \end{equation}

Yine İstanbul ile Ankara örneği için:

• İstanbul'dan Ankara'ya: 108.9°
• Ankara'dan İstanbul'a: 291.4°

Kaynaklar:

1. Küresel kosinüs kanunu
2. Geographic Distance and Azimuth Calculations